
Pythagorejská matematika
"Před současnou tyranií materialistického, mechanického modelu našeho vesmíru moudří lidé všech tradičních kultur považovali svět za souvislé spektrum." Keith Critchlow
Pythagorova matematika
Manly P Hall v knize The Secret Teachings of All Ages píše: "Pythagorejci prohlásili aritmetiku za matku matematických věd. To dokazuje skutečnost, že geometrie, hudba a astronomie jsou na ní závislé, ale nezávisí na nich. Pythagorejci také prokázali, že před astronomií byla aritmetika, protože ta závisí na geometrii i hudbě. Velikost, forma a pohyb nebeských těles je dána použitím geometrie; jejich harmonii a rytmus pomocí hudby. "
V tomto článku se znovu ponoříme do základní vědy o Quadriviu - o čísle. Konkrétně se podíváme na počet a aritmetiku, jak to učil Pythagoras před více než 2500 lety. Pamatujte, že atributy čísel neodmyslitelně patří hudebním měřítkům, oběžným drahám planet, kosmickým časovým cyklům a mnoha dalším věcem. Číslo je tedy kořenem harmonicko-geometrického tvaru vlny vesmíru.
Pythagoras definoval číslo jako rozšíření a energii generativních důvodů obsažených v Monadovi . Bůh Pythagoras byl Monad , "ten, který je vším" a byl znázorněn kruhem. Stejně jako všechny polygony pocházejí z kruhu a všechny polyhedry pocházejí z sféry, všechno ve skutečnosti pochází od Monada , "Nejvyšší mysl distribuovaná po všech částech Vesmíru - Příčina všech věcí, Inteligence všech věcí a Moc ve všech věcech. "
Množství a velikost
Číslo je termín aplikovaný na všechny číslice a jejich kombinace. Věda o matematice má dvě části: mnohost a velikost.
Mnohost odkazuje na součásti věci.
Mnoho lidí má dvě části: to je způsob, jakým se věc vztahuje k sobě, a způsob, jakým věc souvisí s jinými věcmi. V Pythagorově pohledu má vztah k sobě přednost před vztahem k ostatním.
To znamená, že je mnohem důležitější znát a porozumět svému vlastnímu já - vlastní mysli, motivacím, očekáváním, vírám, emocím a myšlenkám, než se snažit porozumět tomu druhému.
"Nejprve se poznej." Pak poznáte ostatní.
Znalost mysli je znalost stvoření.
Velikost se týká relativní velikosti nebo hustoty věci.
Existují dvě části velikosti: Velikost, která je nehybná, a velikost, která je pohyblivá. V Pythagorově pohledu má stacionární velikost přednost před pohyblivou velikostí.
To znamená, že existují dva aspekty nás a vesmíru. Prvním je metafyzický aspekt "Zdroje"-ten, který je nehybný, stabilní, stále pravdivý, věčný-Duch. Druhým je fyzický materiální aspekt - to, co je pohyblivé, proměnlivé, cyklické - tělo.
Stacionární, jako zdroj, nebo ten, který přišel jako první, bude mít vždy přednost před pohyblivými, přechodnými materialistickými aspekty reality, ať už jsou to naše těla samotná nebo dočasné aspekty života: materiální statky, bohatství, zaměstnání, měnící se vztahy , roční období, věk ... atd.
Manly P Hall nám říká: "Množství i velikost byly ohraničeny obvodem mysli." To znamená, že když mluvíme o "věci", nemluvíme striktně o číslicích. Na jedné úrovni mluvíme o mysli samotné - o vědomí a perspektivách každé lidské bytosti. Na jiné úrovni mluvíme o vesmíru samotném - o kosmickém vědomí a o tom, jak se části vesmíru vztahují k jiným částem.
Bude zdůrazněno znovu a znovu: Jakákoli studie počtu má mnohem méně společného s kvantitami a výpočty a mnohem více s rozpoznáváním symboliky za čísly a toho, jak představují různé aspekty vědomí, duchovní evoluce a stvoření a evoluce vesmíru prostřednictvím zvuku, vibrací a vln.
Liché a sudé
Existují dva řády čísla: liché a sudé. John Michell píše: "Rozdělení čísel na lichá a sudá odráželo rozdělení vesmíru na kladně a záporně nabité prvky." 1
Zde nemluvíme jen o kladných a záporných nábojích v elektřině nebo o kladných a záporných pólech magnetu, ale mluvíme o polaritě vědomí - pozitivních a negativních aspektech našich myšlenek, přesvědčení a pocitů.
Pozitivní aspekty nás přibližují k jednotě a zahrnují harmonii a řád. Negativní aspekty nás odvádějí dále od jednoty - zvyšují naši separaci a zahrnují chaos a nepořádek. Tyto pozitivní a negativní aspekty mohou zjevně existovat v nekonečném spektru velikosti a množství a oba jsou nedílnou součástí reality.
Toto prvotní oddělení od Jednoty - Monad - se nazývá Dyad a je reprezentováno číslem 2.
Pythagorejci považovali lichá čísla za určitá a mužská. Považovali sudá čísla - jejichž prototypem byl Dyad - za neurčitá a ženská.
Lichá čísla
Liché číslo nelze dělit stejně, protože jednota nebo 1 zůstává vždy nedělitelná.
Například:
9 = 4 + 1 + 4
19 = 9 + 1 + 9
153 = 76 + 1 + 76 ... atd.
Je užitečné začít takto vidět lichá čísla. Každé liché číslo se točí kolem centrální osy jednoty. Ačkoli je číslo odděleno nebo zlomeno, zachovává si své spojení s jednotou. Ve skutečnosti se její části neustále točí kolem jednoty jako voda víří kolem stoky nebo jako pes honí ocas, krouží kolem dokola a v případě čísel nikdy nepřestává. To mu dává kvalitu pohybu a akce - tedy reprezentováno aktivním mužským principem.
Pokud je navíc liché číslo rozděleno na dvě části, jedna část bude vždy lichá a druhá sudá.
Například:
9 = 4 + 5
19 = 9 + 10
153 = 76 + 77 ... atd.
Manly P Hall nám říká, že Unity, neboli 1, bylo považováno za androgynní číslo, účastnící se jak mužských, tak ženských atributů; v důsledku toho liché i sudé. Z tohoto důvodu to Pythagorejci nazývali rovnoměrně lichým.
Sudá čísla
Sudý počet lze rozdělit na dvě stejné části, které jsou vždy buď liché, nebo obě sudé.
Například:
10 = 5 + 5
144 = 72 + 72
360 = 180 + 180
Můžete vidět, jak sudá čísla obsahují kvalitu pasivity. Jsou si rovni a statičtí. Neobsahují přirozený pohyb lichých čísel, která se neustále otáčejí a pokoušejí se vyvážit své části. Sudá čísla tedy představují pasivní ženský princip.
Třídy lichých čísel
Existují tři obecné třídy lichých čísel: nekompozitní, kompozitní a nekompozitní-kompozitní.
Nekomponovaná čísla jsou prvočísla. Nemají jiného dělitele než sebe a jednotu.
Příklady jsou: 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41 ... atd.
Další informace o prvočíslech najdete v článku 9.
Složená čísla jsou dělitelná nejen sebou a jednotou, ale také nějakým jiným číslem.
Příklady jsou: 9, 15, 21, 25, 27, 33, 39, 45, 51, 57 ... atd
15 je dělitelné 15 a 1, ale také 3 a 5.
39 je dělitelné 39 a 1, ale také 3 a 13.
57 je dělitelné 57 a 1, ale také 3 a 19.
Incomposite-Composite numbers have no Společný dělitel, ačkoli each of each is possible of division, such as 9 and 25.
To znamená, že jsou dělitelné samy sebou a jednotou, a také 1 jediné další číslo.
Protože mají jednotlivé dělitele, nazývají se složené.
Protože nemají společného dělitele (jako například společný 3 výše), nazývají se nekompozitní.
Třídy sudých čísel
Existují tři obecné třídy sudých čísel: sudé-sudé, sudě-liché a liché-sudé.
Rovnoměrná a sudá čísla jsou v jednotném poměru. Tato čísla lze snížit na polovinu a poloviny znovu snížit na polovinu zpět do jednoty.
Například:
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024 ... atd.
Př. 128/2 = 64; 64/2 = 32; 32/2 = 16; 16/2 = 8; 8/2 = 4; 4/2 = 2; 2/2 = 1
Rovnoměrná sudá čísla mají určité jedinečné vlastnosti. Součet libovolného počtu výrazů, ale posledního členu, se vždy rovná poslednímu členu minus jeden.
Například:
Součet prvních 2 výrazů (1 + 2 = 3) se rovná třetímu členu (4) mínus 1 (3), nebo:
Součet 1 st , 2 nd , 3 rd a 4 th podmínek (1 + 2 + 4 + 8 = 15) se rovná 5 th výraz (16) minus 1 (15).
Součet výrazů 1 až 10 = 1023. To se rovná 11. členu (1024) mínus 1 = 1023.
To platí pro všechny podmínky v této sérii.
Tato rovnoměrně rovnoměrná řada představuje proces zdvojení pozorovaný při dělení buněk a struktuře oktáv.
Pamatujte, že čísla nejsou statické "věci". Představují procesy .
Rovnoměrně lichá čísla jsou čísla, která po rozpůlení nejsou schopna dalšího půlení. Jsou tvořeny tak, že vezmeme lichá čísla v pořadí a vynásobíme je 2.
Lichá čísla 1, 3, 5, 7, 9, 11 vytvářejí sudá lichá čísla 2, 6, 10, 14, 18, 22.
Počínaje 2 je každé čtvrté číslo sudě liché.
Rozdělené číslo je dividenda. Číslo, které dělí, je dělitel. Výsledkem rozdělení je kvocient.

Například: V 360/6 = 60 je 360 dividenda. 6 je dělitel. 60 je kvocient.
Pokud je dělitel lichý, je podíl vždy sudý. Například:
18/3 (lichý dělitel) = 6 (sudý podíl)
Pokud je dělitel sudý, je podíl vždy lichý. Například:
18/2 (sudý dělitel) = 9 (lichý kvocient)
Každý termín v řadě je také polovinou součtu výrazů na obou stranách. Například:
10 je polovina součtu výrazů na obou stranách (14 + 6 = 20).
18 je polovina součtu výrazů na obou stranách (22 + 14 = 36) ... atd.
Lichá-lichá nebo nerovnoměrně sudá čísla jsou kompromisem mezi sudými a sudými čísly. Na rozdíl od rovnoměrně rovnoměrných nemohou být rozpůleni zpět k jednotě; a na rozdíl od rovnoměrně lichých jsou schopni více než jedné dělení na polovinu.
Například: 24 24/2 = 12 12/2 = 6 6/2 = 3
Tři další třídy sudých čísel
Existují tři další třídy sudých čísel: superperfektní, nedostatečné a dokonalé.
Superperfektní čísla mají součet jejich zlomkových částí větší než oni sami. Například:
Číslo 24:
½ z 24 = 12; ¼ z 24 = 6; 1/3 z 24 = 8; 1/6 z 24 = 4; 1/12 z 24 = 2; 1/24 = 1
Součet těchto částí (12 + 6 + 8 + 4 + 2 + 1) = 33; který je větší než 24.
Nedostatečná čísla jsou čísla, která mají součet zlomkových částí menší než oni sami. Například:
Číslo 14:
½ ze 14 = 7; 1/7 ze 14 = 2; 1/14 = 1
Součet částí (7 + 2 + 1) = 10, což je méně než 14.
Dokonalá čísla jsou ta čísla, která mají součet jejich zlomkových částí rovný sobě. Například:
Číslo 28:
½ z 28 = 14; ¼ z 28 = 7; 1/7 z 28 = 4; 1/14 z 28 = 2; 1/28 = 1
Součet částí (14 + 7 + 4 + 2 + 1) = 28, což se rovná 28.
Perfektní čísla jsou extrémně vzácná.
Mezi 1 a 10 = 6 je pouze jeden
Jedna mezi 10 a 100 = 28
Jedna mezi 100 a 1000 = 496
Jedna mezi 1000 a 10 000 = 8128
5 th dokonalé číslo = 33550336
"Dokonalá čísla jsou krásné obrazy ctností, které jsou určitými médii mezi přebytkem a vadou." Naopak lze nalézt nekonečné množství nadbytečných a zmenšených čísel, ani nejsou uloženy v žádné spořádané sérii ani nejsou generovány z určitého konce; a proto mají velkou podobnost se zlozvyky, které jsou četné, nepřiměřené a neurčité. " Thomas Taylor, teoretická aritmetika
Teorie čísel pythagorovské matematiky může být jednou z nejsušších informací obsažených v projektu diplomové práce Kosmické jádro, ale je zahrnuta, protože je nutné pochopit, jaký velký význam mělo číslo ve starověké a esoterické filozofii a jak čísla nebyla vnímána jako množství, ale jako symboly obsahující různé kvality. Tyto vlastnosti počtu byly přirovnávány ke kvalitám našich myšlenek, emocí a činů.
U jakékoli myšlenky, emoce nebo akce můžete uvažovat o jejích kvalitách. Obsahuje harmonii? Přináší vám to mír? Hněvá tě to? Cítíte se nadřazeně? Nižší? Vyvolává ve vás touha ublížit něčemu nebo sobě? Vyvolává to ve vás touhu pomoci? Cítíte se mocní? Bezmocný? Strach? Sebejistý? Žárlivý? Soucitný? Zmatený? Povznesený?
Otázka, jak zpochybnit své přesvědčení, myšlenky, emoce a činy, jakmile nastanou, je nejdůležitější lekcí, kterou si z těchto informací můžete odnést. Jaké myšlenky nás přivádějí zpět k jednotě a jaké myšlenky nás oddělují od ostatních nebo od nás samotných? Jak blízko jsou tyto myšlenky jednotě a jak daleko? Čísla jsou symboly těchto atributů našeho vědomí - našich myšlenek, emocí, přesvědčení, očekávání a činů.
Dokonalá čísla jsou považována za božské ctnosti - čisté, nesobecké myšlenky a záměry, které nás vrací přímo k jednotě - myšlenky, emoce a činy, které obsahují dokonalou rovnováhu moudrosti a soucitu, akce a pasivity a síly a jemnosti.
Gnomoni
"Pythagoras učil, že zkušenost života v konečném, omezeném těle byla specificky za účelem objevování a projevování nadpřirozené existence v konečném." Soustředění by tedy mělo být také na samotném konečném, aby se zjistilo, jak by tento konečný mohl ve své podstatě obsahovat sílu k vyjádření nekonečna. To neznamená koncentraci na konečné, materiální efekty, ale na abstraktní principy odhalené v konečném světě a na Příčiny, které vytvářejí a podporují toto ztělesnění. Pythagorova matematika byla proto omezena na celá čísla, tj. Definovatelné, zastavené stavy a hledané univerzální výrazy s měřitelným geometrickým rámem čtverce, hlubokým symbolem konečné dokonalosti. - Robert Lawlor, Sacred Geometry: Philosophy & Practice
Gnomonický růst je libovolný údaj, který po přidání k jinému obrázku zanechá výsledný obrázek podobný originálu.
To je spojeno s Scale Invariance neboli Fraktální podobností, která byla probrána v článku 2 a bude podrobněji rozebrána v dalších článcích.
"Některé věci netrpí žádnou jinou než velikostí, když rostou": Toto je princip gnomonického růstu nebo invariance rozsahu.

Mohou existovat gnomonické spirály, jako je zlatá spirála; tvary, jako jsou proporcionální obdélníky odmocniny; čísla; architektura; a živé systémy, jako je Fibonacciho posloupnost, která se v přírodě hojně nachází.
Zlatá spirála je na obrázku níže:

Krátce probereme gnomonická čísla týkající se pythagorovské matematiky a připomeneme si, že starověcí filozofové jako Pythagoras, Platón a Euclid neměli k práci číslice, ale při studiu čísel používali malé oblázky. Pomocí této metody je mnohem snazší pochopit geometrickou povahu čísel.
Trojúhelníková čísla
Trojúhelníková čísla se zvyšují trojúhelníkovým způsobem, například 1, 3, 6, 10, 15, 21 ... atd.

Trojúhelníkové číslo se skládá ze všech čísel od jednoty až po daný limit.
Série, kterou tvoří, je:
3 (= 1 + 2)
6 (= 1 + 2 + 3)
10 (= 1 + 2 + 3 + 4)
15 (= 1 + 2 + 3 + 4 + 5)
21 (= 1 + 2 + 3 + 4 + 5 + 6) a tak dále.
Když jsou uspořádány pomocí oblázků, tvoří trojúhelníky.
Obdélníková čísla
Obdélníková čísla se zvyšují hudebním způsobem na základě oktáv, například 2, 6, 12, 20. Když jsou uspořádány pomocí oblázků, vytvářejí obdélníky.

Čtvercová čísla
Čtvercová čísla se skládají ze dvou po sobě jdoucích trojúhelníkových čísel, například 1, 4, 9, 16.

Například:
4 = 1 + 3
9 = 6 + 3
16 = 10 + 6 ... atd.
Tato čísla jsou doslovnými 'čtverci' čísel:
2 2 = 4
3 2 = 9
4 2 = 16
5 2 = 25... atd.
Když jsou uspořádány pomocí oblázků, vytvářejí čtverce.
Krychlová čísla
Krychlová čísla jsou doslovné "kostky" čísel, například 1, 8, 27, 64, 125 ... atd.

Například:
2 3 = 8
3 3 = 27
4 3 = 64
5 3 = 125
Když jsou uspořádány pomocí oblázků ve třech rozměrech, vytvářejí kostky.
Lambda
Lambda je numericko-geometrická postava, kterou studovali staří Řekové. To bylo popsáno Plato v Timaeus jako 'Světová duše'.

Platón uvádí, že Bůh stvořil kosmickou duši pomocí dvou matematických proužků 1, 2, 4, 8 a 1, 3, 9, 27.
Tyto dva pásy sledují tvar obráceného "V" nebo "platonické lambdy". Lambda je 11 th písmeno řecké abecedy. Je trojúhelníkové povahy, jako tetraktys diskutované níže. Trojúhelníkový tvar představuje jeho božskou povahu.
"Platón má spojitou geometrickou proporci jako nejhlubší kosmickou vazbu." Světová duše ve svém Timaeusovi spojuje do jedné harmonické rezonance srozumitelný svět forem (včetně čisté matematiky) nahoře a viditelný svět hmotných předmětů dole, přes 1, 2, 4, 8 a 1, 3, 9, 27 série. "2
Výsledkem Platonovy světové duše je Lambda - rozšířená souvislá geometrická proporce.

První řada: 1, 2, 4, 8 je zdvojovací sekvence. Jak jsme diskutovali výše, sudá čísla jsou spojena s pasivním ženským principem.
Druhá řada: 1, 3, 9, 27 je trojnásobná sekvence. Tato lichá čísla jsou spojena s aktivním mužským principem.
Tyto dvě řady dohromady vytvářejí celou škálu hudebních poměrů - tedy oktávu (2: 1), pátou (3: 2), čtvrtou (4: 3) a celý tón (9: 8). Podrobně to probereme v dalších článcích.
Robert Lawlor vysvětluje: "V aritmetické progresi je sčítání prostředkem růstu, zatímco v progresi zvané" geometrická "(příkladem je 2, 4, 8, 16 ...) se každý následující termín odvíjí vynásobením prvním termínem . Sčítání a násobení tedy zůstávají našimi dvěma nejefektivnějšími matematickými metaforami pro popis organického růstu na jedné straně a fyzické nebo gnomonické akumulace na straně druhé.
Typ progrese, který kombinuje jak aditivní, tak multiplikační růstové postupy ostatních dvou progresí, se nazývá "harmonický". Nejdůležitější a nejzáhadnější charakteristikou této formy harmonické, proporcionální progrese je skutečnost, že inverzní k jakékoli harmonické progresi je aritmetická progrese. 2, 3, 4, 5... je tedy vzestupná aritmetická posloupnost, zatímco inverzní řada (1/2, 1/3, ¼, 1/5...) je sestupná harmonická posloupnost.
Tyto dvě paralelní, ale inverzní progrese nejenže poskytují základy hudby, ale obecněji poskytují matematický model, pomocí kterého lze zkoumat komplementární nebo protichůdné symetrie dualizovaného, přesto harmonicky integrovaného celku. Z tohoto důvodu byla hudební metafora základním kamenem starověké filosofie, aplikovatelné na fyzické i metafyzické oblasti. "
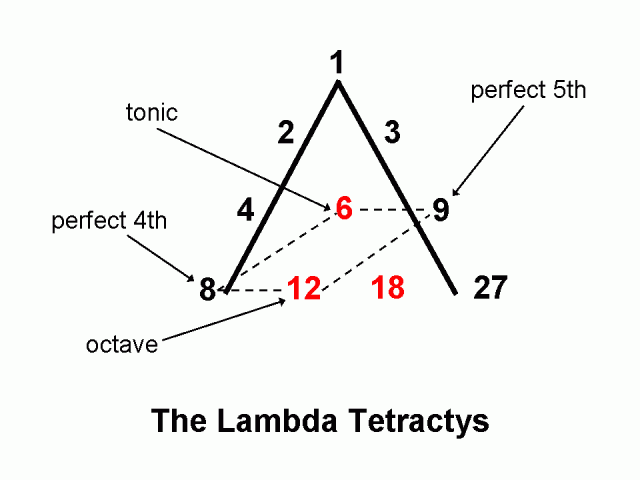
Robert Lawlor nám říká: "Pythagorovi je připsáno, že jako první vytvořil vztah mezi číselnými poměry a zvukovými frekvencemi. Celé číselné poměry pro určování souhláskových zvuků v hudebním měřítku jsou buď čerpány z nebo jsou násobky čísel ve dvou progresích Lambdy. "
"Platónovým evidentním záměrem," uvádí John Michell o Lambdě, "bylo identifikovat číslo jako archetyp stvoření a upozornit na ta konkrétní čísla, která tvoří jeho jádro a která v různých kombinacích generují celé pole čísel."
Tetraktys
Tetraktys je další početní-geometrické postava, která je spojena s Pythagorovy školy. Uvedli jsme to v předchozích článcích.
Freddy Silva píše: "I když je tetractys připisován Pythagorasovi, lze jej vysledovat až k hinduistům a před nimi je věcí dohadů. Stejně jako Květ života je jisté, že je toto číslo spojeno s tvůrčím procesem.
Theon of Smyrna, proslulý starověký učenec, prohlásil, že deset teček tetractysů představuje deset Božích slov. Pro křesťany tato "slova" znamenala Desatero přikázání; do hebrejštiny, deseti sfér Stromu života. Numerická symbolika tetractys však také odpovídá hinduistickému modelu devíti kobr kolem Brahmy, egyptské Grand Ennead kolem Atumu a kabalistickým devíti legiím úhlů kolem Skrytého Boha. "
Skládá se z deseti bodů uspořádaných jako rovnostranný trojúhelník. Stejně jako na Lambdě představuje trojúhelníková forma svou božskou povahu.

Tyto tetraktys je "kosmologický model založený na úplnost deset bodů odvíjející se ve čtyřech úrovních s cílem popsat univerzální vytvoření procesu." 3
Tyto tetraktys je reprezentace Decad - čísla 1-10. Skládá se ze 4 úrovní.
Všimněte si, že 10 = 1 + 2 + 3 + 4.
Tyto čtyři úrovně představují zvyšující se hustotu 4 prvků: země (nejhustší), voda, vzduch a oheň (nejméně husté).

Čtyři úrovně také definují rozvinutí prostoru: bod, čára, povrch a objem: 1D, 2D, 3D a 4D.

Tento symbol je metaforou toho, jak se archetypy 1-10 rozvíjejí a oblékají hmotou, aby se projevily jako viditelné vzory přírody.
Tyto tetraktys také drží geometrii všech pěti platonické pevné látky a geometrii hudby. Čísla 1, 2, 3 a 4 zapouzdřují zlomkové délky vibrujícího řetězce, který vytváří přirozenou 7tónovou hudební stupnici: oktáva (1: 2), dvojitá oktáva (1: 4), čtvrtá (3: 4) a pátý (2: 3). To jsou harmonické, které řídí tvorbu.

Čtyři úrovně také odkazují na různé perspektivy pohledu na jakékoli téma:
Čtyři úrovně také odkazují na čtyři úrovně znalosti. Oni jsou:
- Smyslové údaje - "matoucí množství památek, zvuků, pocitů, vůní, chutí atd., Čistý rozdíl".
- Uznání - získání informací
- Znalosti - schopnost rozpoznávat nebo rozlišovat a souhlasit se sdílenými znalostmi za účelem zjištění pravdy.
- Moudrost - ukázněná čtvrtá fáze - destilace znalostí, která odkazuje na hledání základních hodnot, které nabízejí sjednocující celistvost.
Michael Schneider nám říká: "Pythagorejci si uvědomili, že Tetraktyové představují soubor, jednotu, souhrn celku, který chápal úplnost matematiky a archetypy, které se projevovaly jako viditelné formy světa."
John Michell píše: " Tetractys , trojúhelníková forma čísla 10, měla pro Pythagorejce stejný význam, jaký má diagram stromu života v židovské mystice (diskutováno v článku 6), přičemž oba jsou považovány za symboly vesmíru a čísla 1 až 4, z nichž je složena, byla údajně u kořene veškerého stvoření. "

Posvátná abeceda Pythagorejců
Jako bonusovou část zahrnu zajímavé hodnocení posvátné Pythagorovy abecedy, jak ji popsala Anne Macaulay v Homage to Pythagoras - Pythagorova definice Boha .
Macaulay píše: "Pythagorejci byli jedineční v tom, že používali písmena abecedy jak jako číslice (rys společný všem raným abecedním zvyklostem), tak jako geometrickou symboliku. Geometrie ve známé pythagorejské formě je pro řecké Pythagorejce jedinečná, takže další myšlenkou bylo, zda byla abeceda v předliterární posvátné formě kořenem megalitické kultury. Tato myšlenka dělá z abecedy numero-geometrický systém, který byl také použit pro základní prvky řeči (samohlásky a souhlásky). Pokud by existovala dřívější posvátná forma, pak by nebyla použita k psaní vulgárního jazyka.
Posvátná abeceda je starověký systém, ve kterém byly číslice a geometrické prvky reprezentovány geometrickými symboly; ke každému z těchto znaků byl přidán jeden zvuk (samohláska nebo souhláska), aby se vytvořila jména odpovídající jejich významným geometrickým obrazcům. Zde posuzujeme jméno boha Apollóna. Apollo představovalo transcendentní princip. To bylo v protikladu k Dionýsovi - božskému principu v jeho vzniku nebo stání. Dionýsos musí být roztrhán na kusy a obětován Titány, poté znovu sestaven a zapamatován. Toto je Apollo - to, co bylo transformováno
A = kruh o průměru deset jednotek (alfa = 1. písmeno)
P = kruh s obvod 17 jednotek (pi = 17 th písmeno)
O = kruh s obvod 16 jednotek (omikron = 16 th písmeno)
L = obdélníku o stranách 3 x 4 (lambda = 12 th písmeno)
N = kruh s obvodem 14 jednotek; jeho průměr je 4,4545, s použitím pi = 22/7 (nu = 14 th písmeno)
Numericko-geometrické hodnoty písmen jména Apollo tvoří stručnou a dobře definovanou figuru. Můžeme tedy usoudit, že Apollo je jméno odvozené od posvátné numero-geometrické abecedy z geometrického útvaru, který byl sám odvozen z astronomických pozorování cirkumpolárních hvězd a měsíce. Sekundární rozměry obrázku jsou množinou proporcí stupnice a základními akustickými zákony.
Apollo, bůh odvozený z geometrické figury, není zbožštěným hrdinou ani archetypálním kmotrem, ale syntézou pozorovaných faktů o vztahu hvězd, měsíce a slunce k zemi; je to časový úsek a kalendář; je to vyjádření nebeských zákonů z hlediska geometrických a matematických prvků, které samy vykazují absolutní zákony; a tyto zákony platí i pro hudbu.
Existence tohoto proudu moudrosti Apolla vysvětluje problém, proč byli pozdější učitelé, Socrates a Platón atd. Ve své době známí jako Pythagorejci, ale neexistoval žádný přímý prostředník, který by jim mohl předat Pythagorovo učení. Vztah je v tom, že všichni veřejně učili aspekty moudrosti Apolla.
Možná nejdůležitější zprávou Apolla pro nás dnes je znovu si uvědomit v praxi harmonii, která prostupuje veškerým bytím. "